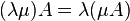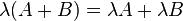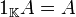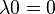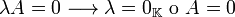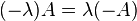Sean  y
y 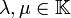 ,
donde
,
donde  es un campo, entonces se cumplen las
siguientes propiedades para la operación producto por un escalar
es un campo, entonces se cumplen las
siguientes propiedades para la operación producto por un escalar
 y
y 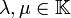 ,
donde
,
donde  es un campo, entonces se cumplen las
siguientes propiedades para la operación producto por un escalar
es un campo, entonces se cumplen las
siguientes propiedades para la operación producto por un escalar- Asociatividad
Demostración. Dada la definición de la operación se sigue el
resultado ya que 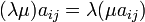 debido a que
debido a que  para todo
para todo 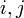 .
.
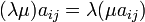 debido a que
debido a que  para todo
para todo 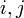 .
.- Distributividad respecto de la suma de matrices
Demostración Dada la definición de la operación se sigue el
resultado ya que  debido a que
debido a que  para todo
para todo 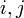 .
.
 debido a que
debido a que  para todo
para todo 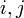 .
.- Distributividad respecto de la suma en el campo
Demostración Dada la definición de la operación se sigue el
resultado ya que 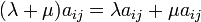 debido a que
debido a que  para todo
para todo 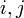 .
.
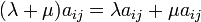 debido a que
debido a que  para todo
para todo 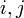 .
.- Producto por el neutro multiplicativo del campo
Demostración Dada la definición de la operación se sigue el
resultado ya que 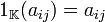 debido a que
debido a que  para todo
para todo 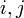 .
.
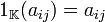 debido a que
debido a que  para todo
para todo 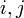 .
.Por como se definió la operación de producto por escalares se dice que
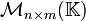 es cerrado bajo producto por escalares. Con éstas propiedades y las de
la adición se tiene que
es cerrado bajo producto por escalares. Con éstas propiedades y las de
la adición se tiene que 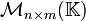 es un espacio vectorial con las operaciones de
suma y producto por escalares definidas antes.
es un espacio vectorial con las operaciones de
suma y producto por escalares definidas antes.
En el caso de que las entradas y los escalares no estén en un campo sino en un anilloanillo con uno, se dice que 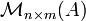 es un módulo sobre
es un módulo sobre 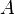 . entonces no necesariamente existe
el neutro multiplicativo. En caso de que exista, con lo cual el anillo
es un
. entonces no necesariamente existe
el neutro multiplicativo. En caso de que exista, con lo cual el anillo
es un
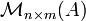 es un módulo sobre
es un módulo sobre 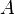 . entonces no necesariamente existe
el neutro multiplicativo. En caso de que exista, con lo cual el anillo
es un
. entonces no necesariamente existe
el neutro multiplicativo. En caso de que exista, con lo cual el anillo
es un Ahora, a partir de las propiedades básicas se puede demostrar inmediatamente que
Demostración Dada la definición de la operación se sigue el
resultado ya que 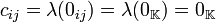 para todo
para todo 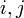 .
.
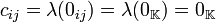 para todo
para todo 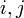 .
.
Demostración Dada la definición de la operación se sigue el
resultado ya que  para todo
para todo 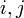 debido a que
debido a que  para todo
para todo 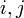 .
.
 para todo
para todo 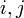 debido a que
debido a que  para todo
para todo 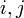 .
.
Demostración Dada la definición de la operación se sigue el
resultado ya que como en un campo no hay divisores de cero entonces 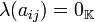 para todo
para todo 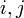 implica que
implica que  o
o 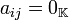 para
todo
para
todo 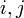 ,
i.e.
,
i.e.  .
No es posible un caso en el que sólo algunas entradas de la matriz sean
cero y el escalar sea no nulo ya que en esos casos estaríamos diciendo
que hay divisores de cero y llegaríamos a una contradicción, ya que la
suposición es que las entradas y los escalares están en un campo.
.
No es posible un caso en el que sólo algunas entradas de la matriz sean
cero y el escalar sea no nulo ya que en esos casos estaríamos diciendo
que hay divisores de cero y llegaríamos a una contradicción, ya que la
suposición es que las entradas y los escalares están en un campo.
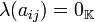 para todo
para todo 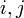 implica que
implica que  o
o 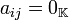 para
todo
para
todo 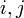 ,
i.e.
,
i.e.  .
No es posible un caso en el que sólo algunas entradas de la matriz sean
cero y el escalar sea no nulo ya que en esos casos estaríamos diciendo
que hay divisores de cero y llegaríamos a una contradicción, ya que la
suposición es que las entradas y los escalares están en un campo.
.
No es posible un caso en el que sólo algunas entradas de la matriz sean
cero y el escalar sea no nulo ya que en esos casos estaríamos diciendo
que hay divisores de cero y llegaríamos a una contradicción, ya que la
suposición es que las entradas y los escalares están en un campo.
Demostración Dada la definición de la operación se sigue el
resultado ya que 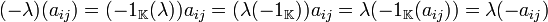 debido a que
debido a que  para todo
para todo 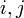 .
.
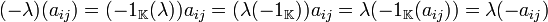 debido a que
debido a que  para todo
para todo 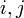 .
.
Este último resultado permite usar la notación  sin riesgo de ambigüedad.
sin riesgo de ambigüedad.
 sin riesgo de ambigüedad.
sin riesgo de ambigüedad.
Operaciones de Matrices
Dadas dos matrices de la misma dimensión, A=(aij)
y B=(bij), se define la matriz suma como: A+B=(aij+bij).
Es decir, aquella matriz cuyos elementos se obtienen: sumando los
elementos de las dos matrices que ocupan la misma misma posición.

Producto de un escalar por una matriz
Dada una matriz A = (aij)
y un número real k  R, se define el producto de un número real por
una matriz: a la matriz del mismo orden que A, en la que cada elemento
está multiplicado por k.
R, se define el producto de un número real por
una matriz: a la matriz del mismo orden que A, en la que cada elemento
está multiplicado por k.
 R, se define el producto de un número real por
una matriz: a la matriz del mismo orden que A, en la que cada elemento
está multiplicado por k.
R, se define el producto de un número real por
una matriz: a la matriz del mismo orden que A, en la que cada elemento
está multiplicado por k.
k · A=(k aij)

Propiedades
a · (b · A) = (a · b) · A
A  Mmxn,
a, b
Mmxn,
a, b 

 Mmxn,
a, b
Mmxn,
a, b 

a · (A + B) = a · A + a · BA,B  Mmxn
, a
Mmxn
, a 

 Mmxn
, a
Mmxn
, a 

(a + b) · A = a · A + b · A
A  Mmxn
, a, b
Mmxn
, a, b 

 Mmxn
, a, b
Mmxn
, a, b 

1 · A = A
A  Mmxn
Mmxn
 Mmxn
Mmxn
Dos matrices A y B se dicen multiplicables si el número
de columnas de A coincide con el número de filas de B.
Mm
x n x Mn x p = M m x p
El elemento cij de la matriz producto se
obtiene multiplicando cada elemento de la fila i de la matriz A por cada
elemento de la columna j de la matriz B y sumándolos.

Propiedades del producto de matrices
Asociativa:
A · (B · C) = (A · B) · C
Elemento
neutro:
A · I = A
Donde I es la matriz identidad
del mismo orden que la matriz A.
No es Conmutativa:
A · B ≠ B · A
Distributiva del producto
respecto de la suma:
A · (B + C) = A · B + A · C
A · A-1
= A-1 · A = I
Propiedades
(A · B)-1 = B-1 · A-1
(A-1)-1 = A
(k · A)-1 = k-1 · A-1
(A t)-1 = (A -1)t
Cálculo por el método de Gauss
Sea A una matriz cuadrada de orden n. Para calcular la
matriz inversa de A, que denotaremos como A-1,
seguiremos los siguientes pasos:
1º Construir una matriz del
tipo M = (A | I), es decir, A está en la mitad
izquierda de M y la matriz identidad I en la derecha.
Consideremos una matriz 3x3
arbitraria

La
ampliamos con la matriz identidad de orden 3.

2º Utilizando el
método Gauss vamos a transformar la mitad izquierda, A, en la matriz
identidad, que ahora está a la derecha, y la matriz que resulte en el
lado derecho será la matriz inversa: A-1.
F2 - F1


F3 + F2

F2 - F3

F1 + F2

(-1) F2

La matriz
inversa es:


Rango de una matriz: es el número
de líneas de esa matriz (filas o columnas) que son linealmente
independientes.
Una línea es linealmente dependiente
de otra u otras cuando se puede establecer una combinación lineal entre
ellas.
Una línea es linealmente independiente
de otra u otras cuando no se puede establecer una combinación lineal
entre ellas.
El rango de una matriz A se simboliza: rang(A) o
r(A).
Cálculo por el método de Gauss
Podemos descartar una línea si:
- Todos sus coeficientes son ceros.
- Hay dos líneas iguales.
- Una línea es proporcional a otra.
- Una línea es combinación lineal de otras.

F4 es nula
F5 = 2F2 + F1
r(A) = 2.
En general consiste en hacer nulas el máximo número de
líneas posible, y el rango será el número de filas no nulas.

F2 = F2 - 3F1
F3= F3 - 2F1
F3= F3 - 2F1

Por tanto r(A) = 3.
Determinantes
Dada una matriz cuadrada

se llama determinante de A, y se representa por |A| ó
det(A), al número:
(Sn es el grupo de las
permutaciones
del conjunto {1, 2,.. n}, e i(s)
es la signatura de la permutación)
También se suele escribir:

Cálculo de determinantes de órdenes 1, 2 y 3
Es fácil comprobar que aplicando la definición
se tiene: 


En
este
último caso, para acordarnos de todos los productos posibles
y sus correspondientes signos se suele usar la Regla de Sarrus,
que consiste
en un esquema gráfico para los productos positivos y otro para los
negativos:


Cálculo de un
determinante por los adjuntos de una línea
Sea A una matriz cuadrada y aij uno
cualquiera de sus elementos. Si se suprime la fila i y la columna j de
la matriz A se obtiene una submatriz Mij que recibe el
nombre de matriz complementaria del elemento aij.
Dada la matriz

la matriz complementaria del elemento a11
es la matriz que resulta de suprimir en la matriz A la fila 1 y la
columna
1; es decir:

Llamamos menor complementario del elemento aij
al determinante de la matriz complementaria del elemento aij
, y se representa por aij
Se llama adjunto de aij ,
y se
representa por por Aij,
al número (–1)i+jaij.
El determinante de una matriz cuadrada es
igual a la
suma de los elementos de una fila o columna cualquiera, multiplicados
por
sus adjuntos.
Por ejemplo, si desarrollamos un determinante de
orden
n por los adjuntos de la 1ª fila se tiene:
La demostración es muy fácil, basta con aplicar
la definición de determinante a ambos lados de la igualdad.Nota
Esta regla rebaja el orden del determinante que se pretende calcular en una unidad. Para evitar el cálculo de muchos determinantes conviene elegir líneas con muchos ceros
Esta regla rebaja el orden del determinante que se pretende calcular en una unidad. Para evitar el cálculo de muchos determinantes conviene elegir líneas con muchos ceros
Propiedades
de los determinantes
Si todos los elementos de una línea (fila o columna) de una matriz cuadrada se descomponen en dos sumandos, entonces su determinante es igual a la suma de dos determinantes que tienen en esa línea los primeros y segundos sumandos, respectivamente, y en las demás los mismos elementos que el determinante inicial.
Si todos los elementos de una línea (fila o columna) de una matriz cuadrada se descomponen en dos sumandos, entonces su determinante es igual a la suma de dos determinantes que tienen en esa línea los primeros y segundos sumandos, respectivamente, y en las demás los mismos elementos que el determinante inicial.
det (k·L1, L2, L3...) = k·det (L1, L2, L3...)
det (A·B) = det (A) · det (B)
det (L1, L2, L3...) = -det (L2, L1, L3...)
det (0, L2, L3...) = 0
det (L1, L1, L3...) = 0
det (L1, k·L1, L3...) = 0
det (L1, L2, a·L1 + b·L2...) = 0
det (F1 + F2, F2, F3) = det (F1, F2, F3) + det (F2, F2, F3) = det (F1, F2, F3)
det (L1 + k· L2, L2, L3...) = det (L1, L2, L3...) + det (k·L2, L2, L3...) = det (L1, L2, L3...) + 0
Cálculo de determinantes por el método
de Gauss
Se conoce cómo método de Gauss a un
método para facilitar el cálculo de determinantes usando las propiedades
de éstos. Dicho método consiste en hallar un determinante equivalente
(con el mismo valor) al que se pretende calcular, pero triangular. De
esta forma el problema se reduce a calcular un determinante de una
matriz triangular, cosa que es bastante fácil usando las propiedades de
los determinantes.
Para conseguir triangularizar el determinante se
pueden aplicar las siguientes operaciones:
- Permutar 2 filas ó 2 columnas.
- Multiplicar o dividir una línea por un número no nulo.
- Sumarle o restarle a una línea otra paralela multiplicada por un número no nulo.
Aplicación
de las matrices y los determinantes a los sistemas de ecuaciones
lineales

Representación matricial de un s.e.l.
El anterior sistema se puede expresar en forma matricial, usando el producto de matrices de la forma:


Discusión de un s.e.l.: Teorema de Rouché-Fröbenius
Dado un sistema de ecuaciones con matriz de coeficientes A, matriz ampliada A' y rangos respectivos r y r' se verifican:
1. El sistema de ecuaciones es compatible cuando
rango(A)
= rango(A')
2. En caso de compatibilidad existen dos
posibilidades:
Si r = r' = n (nº de incógnitas) Þ
Sistema compatible determinado (una única solución)
Si r = r' < n (nº de incógnitas) Þ
Sistema compatible indeterminado (infinitas soluciones)
Al valor n - r se le llama grado de libertad del
sistema.Resolución de un s.e.l.
a) Regla de Cramer
Es aplicable si el sistema tiene igual número de ecuaciones que de incógnitas (n=m) y es compatible determinado (a un s.e.l. qu cumple estas condiciones se le llama un sistema de Cramer).
El valor de cada incógnita xi se obtiene de un cociente cuyo denominador es el determinate de la matriz de coeficientes, y cuyo numerador es el determinante que se obtiene al cambiar la columna i del determinante anterior por la columna de los términos independientes.
Ejemplo
b) Por inversión de la matriz de coeficientes
Si A·X = B, entonces X = A-1B.
Es aplicable si el sistema tiene igual número de ecuaciones que de incógnitas (n=m) y es compatible determinado.